Q:
Two partners investede Rs. 1250 and Rs. 850 respectively in a business. They distributed 60% of the profit equally and decide to distribute the remaining 40% as the ratio of their capitals. If one partner received Rs. 30 more than the other, find the total profit?
Answer
Let the total profit be Rs.x
60% of the profit = 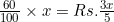
from this part of the profit each gets = Rs.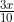
40% of the profit = 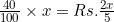
Now, this amount of Rs.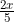 has been divided in the ratio of capitals 1250 : 850 = 25 :17
has been divided in the ratio of capitals 1250 : 850 = 25 :17
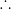 Share on first capital =
Share on first capital = =Rs.\frac{5x}{21})
Share on second capital = =Rs.\frac{17x}{105})
Total money received by 1st investor = ![\inline [\frac{3x}{10}+\frac{5x}{21}]= Rs.\frac{113x}{210}](https://latex.codecogs.com/gif.latex?\inline&space;[\frac{3x}{10}+\frac{5x}{21}]=&space;Rs.\frac{113x}{210})
Total money received by 2nd investor = ![\inline [\frac{113x}{210}+\frac{97x}{210}]=Rs.\frac{97x}{210}](https://latex.codecogs.com/gif.latex?\inline&space;[\frac{113x}{210}+\frac{97x}{210}]=Rs.\frac{97x}{210})
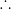 x = 393.75
x = 393.75
Hence total profit = Rs. 393.75
View answer
Workspace
Report Error
Discuss