st Search

Q:

Who is the author of the book ' The Last Word'

Answer

Hanif Qureishi

Workspace

Report Error

View answer Workspace Report Error Discuss

Subject: Books and Authors

Q:

Two partners investede Rs. 1250 and Rs. 850 respectively in a business. They distributed 60% of the profit equally and decide to distribute the remaining 40% as the ratio of their capitals. If one partner received Rs. 30 more than the other, find the total profit?

Answer

Let the total profit be Rs.x

60% of the profit = 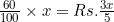$\inline \frac{60}{100}\times x=Rs.\frac{3x}{5}$

from this part of the profit each gets = Rs.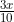 $\inline \frac{3x}{10}$

40% of the profit = 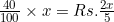$\inline \frac{40}{100}\times x=Rs.\frac{2x}{5}$

Now, this amount of Rs.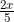 $\inline \frac{2x}{5}$ has been divided in the ratio of capitals 1250 : 850 = 25 :17

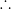$\inline \therefore$ Share on first capital = $\inline (\frac{2x}{5}\times \frac{25}{42})=Rs.\frac{5x}{21}$

Share on second capital = $\inline (\frac{2x}{5}\times \frac{17}{42})=Rs.\frac{17x}{105}$

Total money received by 1st investor = $\inline [\frac{3x}{10}+\frac{5x}{21}]= Rs.\frac{113x}{210}$

Total money received by 2nd investor = $\inline [\frac{113x}{210}+\frac{97x}{210}]=Rs.\frac{97x}{210}$

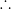$\inline \therefore$ x = 393.75

Hence total profit = Rs. 393.75

Workspace

Report Error

View answer Workspace Report Error Discuss

Subject: Partnership

Q:

A is a working and B is sleeping partners in a business. A puts in Rs. 5000 and B puts in Rs.6000. A receives % of the profit for managing the business and the rest is divided in proportion to their capital. What does each get out of a profit of Rs. 880?

Answer

Total profit = Rs. 880

A's share for managing the business i.e

$\inline 12\frac{1}{2}$ % = $\inline \frac{25\times 880}{200}=Rs.110$

Remaining profit of A and B as per their capital = 880 - 110 = Rs. 770

Ratio of amounts = 5000 : 6000 = 5 : 6

Sum of ratios = 5 + 6 = 11

A's share = $\inline 770\times \frac{5}{11}= Rs.350$

A's total share = 350 + 110 = Rs. 460

B's share = $\inline 770\times \frac{6}{11}=Rs.420$

Workspace

Report Error

View answer Workspace Report Error Discuss

Subject: Partnership

Q:

The ratio of investments of two partners is 11:12 and the ratio of their profits is 2 : 3. If A invested the money for 8 months , find for how much time B invested his money.

Answer

Suppose A invested Rs.11 for 8 months and B invested Rs. 12 for x months.

$\inline \therefore$ Ratio of investments of A and B

= (11 x 8) : (12 x x)

= 88 : 12x

$\inline \therefore$ $\inline \frac{88}{12x}=\frac{2}{3}\Rightarrow x=11$

Workspace

Report Error

View answer Workspace Report Error Discuss

Subject: Partnership

Q:

A and B enter into partnership. A supplies whole of the capital amounting to Rs. 45000 with the condition that the profits to be equally divided and that B pays A interest on half of the capital at 10% per annum, but receives Rs. 120 per month for carrying on the concern.Find their total yearly profit when B's income is one half of A's income.

Answer

Let the total profit be Rs. x

Amount paid to B as salary = (120 x 12)

= Rs.1440

Share of each = $\inline (\frac{x-1440}{2})$

Interest paid by B = $\inline \frac{22500\times 10}{100}=Rs.2250$

Total money received by A = $\inline \frac{x-1440}{2}+2250$

= Rs. $\inline (\frac{x+3060}{2})$

Total money received by B

$\inline [(\frac{x-1440}{2})+1440-2250]= (\frac{x-3060}{2})$

$\inline \Rightarrow \frac{1}{2}-(\frac{x+3060}{2})-(\frac{x-3060}{2})$

$\inline \Rightarrow x=9180$

Workspace

Report Error

View answer Workspace Report Error Discuss

Subject: Partnership

Q:

Three graziers A,B and C rent a piece of pasture for a month. A puts in 27 cattle for 19 days, B 21 for 17 days and C 24 for 23 days. If at the end of the month the rent amount to Rs.237, how much ought to be paid by each.

Answer

A's cattle = 27 x 19 = 513

B's cattle = 21 x 17 = 357

C's cattle = 24 x 23 = 552

Ratio of cattle = 513 : 357 : 552

= 171 : 119 : 184

payment to be made by A = $\inline 237\times \frac{171}{474}$

= Rs.85.50

payment to be made by B = $\inline 237\times \frac{119}{474}$

= Rs.59.50

payment to be made by C = $\inline 237\times \frac{184}{474}$

= Rs.92

Workspace

Report Error

View answer Workspace Report Error Discuss

Subject: Partnership

Q:

Two numbers are 20% and 30% less than the third number . How much percent is the second number less than first?

Answer

Let the third number be 100.

Then, the first number = 100 - 20 = 80 and second number = 100 - 30 = 70.

Difference between the first and second number = 80-70 = 10

$\inline \therefore$ Required percentage = $\frac{10}{80} x 100$ % = 100/8 = 12.5%

Workspace

Report Error

View answer Workspace Report Error Discuss

Subject: Percentage Exam Prep: Bank Exams

Q:

Two pipes A and B can fill a cistern in 4 minutes and 6 minutes respectively . If these pipes are turned on alternately for 1 minute each how long will it take to the cistern to fill?

Answer

As the pipes are operating alternatively, thus their 2 minutes job is = $\frac{1}{4} + \frac{1}{6} = \frac{5}{12}$

In the next 2 minutes the pipes can fill another $\frac{5}{12}$ part of cistern.

Therefore, In 4 minutes the two pipes which are operating alternatively will fill $\frac{5}{12} + \frac{5}{12} = \frac{5}{6}$ Remaining part = $1 - \frac{5}{6} = \frac{1}{6}$

Pipe A can fill $\frac{1}{4}$ of the cistern in 1 minute

Pipe A can fill $\frac{1}{6}$ of the cistern in = $\frac{2}{3}$ min

Therefore, Total time taken to fill the Cistern

4 + $\frac{2}{3}$ minutes.

Workspace

Report Error

View answer Workspace Report Error Discuss

Subject: Time and Work Exam Prep: CAT , Bank Exams , AIEEE
Job Role: Bank PO , Bank Clerk

Searching for "st"

Quick Links