17
Q:
| A) 42.2 mts | B) 33.45 mts |
| C) 66.6 mts | D) 58.78 mts |
Answer: C) 66.6 mts
Explanation:
Explanation:
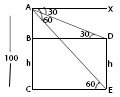
From above diagram
AC represents the hill and DE represents the tower
Given that AC = 100 m
angleXAD = angleADB = 30° (∵ AX || BD )
angleXAE = angleAEC = 60° (∵ AX || CE)
Let DE = h
Then, BC = DE = h, AB = (100-h) (∵ AC=100 and BC = h), BD = CE
tan 60°=AC/CE => √3 = 100/CE =>CE = 100/√3 ----- (1)
tan 30° = AB/BD => 1/√3 = 100−h/BD => BD = 100−h(√3)
∵ BD = CE and Substitute the value of CE from equation 1
100/√3 = 100−h(√3) => h = 66.66 mts
The height of the tower = 66.66 mts.

 Aptitude and Reasoning
Aptitude and Reasoning General Knowledge
General Knowledge Puzzles
Puzzles Interviews
Interviews Technical
Technical Certifications
Certifications Exams
Exams Job
Roles
Job
Roles True or False
True or False Exams
Exams