Height and Distance Questions
FACTS AND FORMULAE FOR HEIGHT AND DISTANCE PROBLEMS
1.In a right angled , where

(i).
(ii).
(iii).
(iv).
(v).
(vi).
2. Trigonometrical Identities :
(i).
(ii).
(iii).
3. Values of T-ratios :
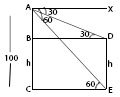
4. Angle of Elevation:

Suppose a man from a point O looks up at an object P, placed above the level of his eye. Then, the angle which the line of sight makes with the horizontal through O, is called the angle of elevation of P as seen from O.
Therefore, Angle of elevation of P from O is =
5. Angle of Depression :

Suppose a man from a point O looks down at an object P, placed below the level of his eye, then the angle which the line of sight makes with the horizontal through O, is called the angle of depression of P as seen from O.
 Aptitude and Reasoning
Aptitude and Reasoning General Knowledge
General Knowledge Puzzles
Puzzles Interviews
Interviews Technical
Technical Certifications
Certifications Exams
Exams Job
Roles
Job
Roles True or False
True or False Exams
Exams